interaktivna geometrija -> krug -> Teorema o tetivnnom četvorouglu (Teorema i Dokaz)
Teorema o tetivnom četvorouglu
TEOREMA: Četvorougao je tetivni ako i samo mu je zbir naspramnih uglova jednak opruženom uglu α + γ= β + δ =180°.
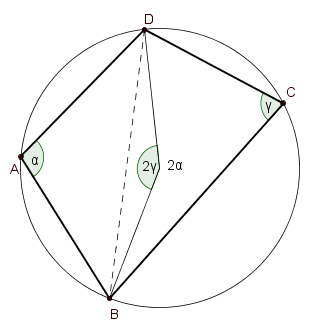
Dokaz: => Pretpostavimo, najpre da je četvorougao ABCD tetivni. Kako
je četvorougao konveksan, temena A i C su sa raznih strana prave
određene dijagonalom BD. Na osnovu posledice o periferijskim uglovima nad istom tetivom, uglovi
BAD i BCD četvorougla su suplementni.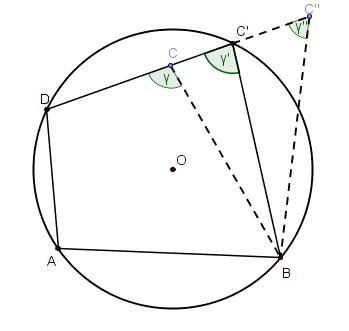
<= Pretpostavimo sada da su naspramni uglovi četvorougla ABCD suplementni. Neka je k krug opisan oko trougla ABD. Treba dokazati da tema C mora pripadati ovoj kružnici.
Ako C nije na kružnici, onda je ili unutar kružnice k ili je van nje.
Pretpostavimo prvo da je unutra. Tada prava CD seče kružnicu u tački C'. Prema prvom delu dokaza, tada je α + γ' =180°, pa kako je α + γ =180°, sledi da je γ = γ' . Međutim, γ je spoljašnji ugao trougla BCC', pa je γ > γ', što dovodi do protivrečnosti. Prema tome tačka C ne može biti u krugu.
Slično se dokazuje da C ne može biti van kruga.