interaktivna geometrija ->krug -> Ugao između tangente i dodirnog poluprečnika (Teorema i Dokaz)
Ugao između tangente i poluprečnika kruga
DEFINICIJA: Prava koja je u ravni jednog kruga, i ima sa krugom samo jednu zajedničku tačku naziva se tangenta toga kruga, a ta tačka zove se dodirna tačka ili tačka dodira.
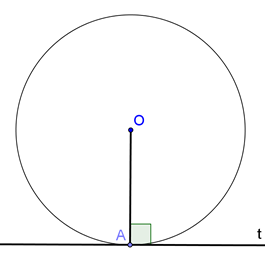
Interaktivno
Još o krugu...

TEOREMA: Prava t je tangenta tog kruga u tački A akko je OA ⊥ t.
Dokaz: => Dokažimo: t tangenta u tački A => t ⊥ OA.
Po Zakonu kontrapozicije (p ⇒ q)⇔(¬q ⇒ ¬p) pretpostavimo da nije t ⊥ OA. Sledi da postoji jedinstvena tačka B ∈ t takva da je OB⊥ t.
Znači ∠ABO=90°. Uočimo trougao ABO, ugao ∠ABO >∠BAO pa je OA > OB tj. r >OB što znači da B pripada krugu, tj.
t nije tangenta.
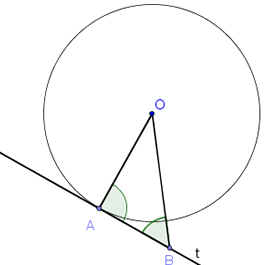
<= Dokažimo: t ⊥ OA => t tangenta u tački A. Za svaku tačku B ∈ t trougao OAB je pravougli sa hipotenuzom OB, pa je OB > OA = r. Dakle, proizvoljna tačka B prave t ne pripada krugu k, pa je t zaista tangenta tog kruga.