Valentina

TEOREMA: Četvorougao ABCD je tangentni ako i samo ako je: AB+CD=BC+AD.

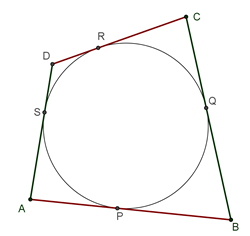
Dokaz: => Pretpostavimo da je četvorougao ABCD tangentni. Neka su P, Q, R, S dodirne tačke ivica AB, BC, CD, DA sa upisanim krugom k. Kako su tangentne duži podudarne, to je: AP=AS; BP=BQ; CQ=CR; DR=DS.
Na osnovu toga je: AP+PB+CR+RD=AS+SD+BQ+QC tj.
AB+CD=AD+BC.

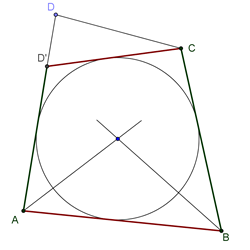
<= Sada dokazujemo obratno tvrđenje. Neka su u četvorouglu ABCD zbirovi naspramnih ivica jednaki. Postoji krug k koji dodiruje ivice AB, BC, i DA tog četvorougla (njegov centar je presek bisektrisa unutrašnjih uglova kod temena A i B četvorougla).
Neka je D' presek druge tangente iz tačke C kruga k i prave AD. Pretpostavimo da je D'≠D i
A - D' - D. Prema već dokazanom delu teoreme važi AB+CD'=BC+D'A, pa kako je po pretpostavci
AB+CD=BC+DA, to je CD'-CD=D'A-DA, tj. CD'=D'A-DA+CD.
Međutim, iz A - D' - D sledi da je CD'=CD-DD' a to je nemoguće na osnovu nejednakosti trougla. Na sličan način dolazimo do kontradikcije i ako je A - D - D'. Dakle, D'=D, tj. krug k dodiruje i četvrtu ivicu četvorougla ABCD.