interaktivna geometrija -> krug -> Teorema o tangentnom uglu (Teorema i Dokaz)
Teorema o tangentnom uglu
TEOREMA: Ugao određen tetivom i tangentom u jednoj krajnjoj tački tetive (tangentni ugao ) nekog kruga podudaran je periferijskom uglu nad tom tetivom.
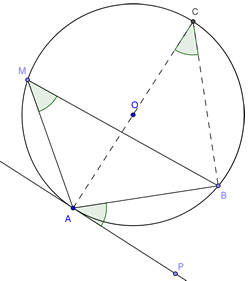
Dokaz: Neka je AMB periferijski ugao nekog kruga nad tetivom AB, AP tangenta tog kruga u tački A tako da je P, M ÷ AB i AC prečnik tog kruga. Tada je AC ⊥ AP (po TEOREMI o uglu između tangente i dodirnog poluprečnika) i AB ⊥ CB (po POSLEDICI o periferijskom uglu nad prečnikom), pa su uglovi PAB i PCB podudarni kao uglovi sa normalnim kracima. Ali na osnovu POSLEDICE o periferijskim uglovima nad istom tetivom su i uglovi AMB i ACB su podudarni , iz čega sledi tvrđenje.