Valentina

interaktivna geometrija ->krug -> Centralni i periferijski ugao (Teorema - Dokaz)

Interaktivno

Teoreme - Dokazi

Centralni i periferijski ugao

Neka je k(O,r) kružnica.
Centralni ugao ove kružnice je svaki ugao čije je teme tačka O (centar kružnice).
Periferijski ugao kruga je ugao čije teme pripada kružnici, a kraci sadrže tetive kruga.

Centralni i periferijski uglovi nekog kruga su jedan drugom odgovarajući ako su nad istom tetivom i iste orijentacije.

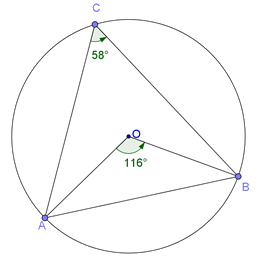
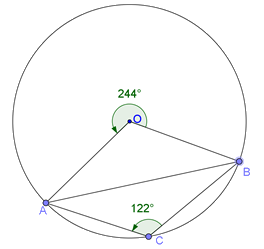
CentralniPeriferijski Ugao CentralniPeriferijski Ugao

TEOREMA: Centralni ugao je dva puta veći od odgovarajućeg periferijskog ugla kruga tj. ako su A, B, C proizvoljne tačke kruga k(O,r) tada je: ∠AOB=2∠ACB.

DOKAZ: Razmotrimo sledeće slučajeve:

1

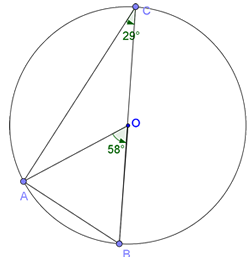1) Centar kruga pripada kraku periferijskog ugla.

Tada je trougao AOC jednakokraki (OA=OC=r) pa su uglovi OAC i ACO podudarni.

U trouglu AOC spoljašnji ugao AOB jednak je zbiru nesusednih unutrašnjih uglova:
∠AOB=∠OAC+∠ACO=2∠ACO=2∠ACB.

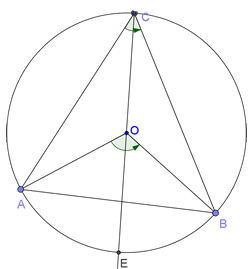CentralniPeriferijski

2) Centar kruga pripada unutrašnjosti periferijskog ugla.

Neka je E druga presečna tačka kruga sa pravom OC.

Tada je (primenjujemo rezultat slučaja 1):

∠AOB=∠AOE+∠EOB=2∠ACO+2∠OCB=2(∠ACO+∠OCB)=2∠ACB
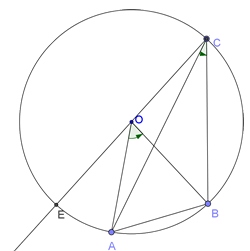Centralni

3) Centar kruga je van periferijskog ugla.

Ponovo na isti način uvedimo tačku E i primenimo rezultat prvog slučaja:
∠AOB=∠EOB -∠EOA=2∠ECB -2∠ECA=2(∠ECB -∠ECA)=2∠ACB.
Interaktivno Još o krugu...